Question

One week a computer store sold a total of 36 computers and external hard drives. The revenue from these sales was 29,820. If computers sold for 1180 and hard drives for 125 per unit, how many of each were sold?

Answer 1

Given:

One week a computer store sold a total of 36 computers and external hard drives.

Let the number of computers = x

And the number of the external hard drives = y

so, we can write the following equation:

`x+y=36\rightarrow(1)`

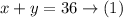
The revenue from these sales was 29,820. If computers sold for 1180 and hard drives for 125 per unit

So, we can write the following equation:

`1180x+125y=29820\rightarrow(2)`

We will solve the equations (1) and (2) to find (x) and (y):

from equation (1):

Substitute (y) from equation (3) into equation (2) and then solve for (x):

`\begin{gathered} 1180x+125(36-x)=29820 \\ 1180x+125*36-125x=29820 \\ 1180x-125x=29820-125*36 \\ 1055x=25320 \\ \\ x=(25320)/(1055)=24 \end{gathered}`

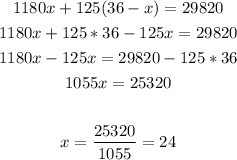
Substitute (x) into equation (3) to find (y):

`y=36-24=12`

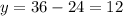
So, the answer will be:

The number of computers sold = 24

The number of hard drives sold = 12