Question

given tan A = 16/63 and that angle A is in Quadrant I, find the exact value of csc A in simplest radical form using a rational denominator

Answer 1

csc A = 65/16

Step-by-step explanation:

The tangent of an angle in a right triangle can be calculated as the opposite side over the adjacent side. It means that we can represent tan A = 16/63 as:

Then, to know the value of csc A, we need to find the hypotenuse of the triangle. So, using the Pythagorean theorem, we get that x is equal to:

`\begin{gathered} x=\sqrt[]{63^2+16^2} \\ x=\sqrt[]{3969+256} \\ x=\sqrt[]{4225} \\ x=65 \end{gathered}`

Now, the cosecant of an angle is equal to:

`\csc A=\frac{Hypotenuse}{Opposite\text{ side}}`

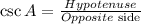
So, replacing the hypotenuse by the value of x and the opposite side by 16, we get:

`\begin{gathered} \text{csc A =}(x)/(16) \\ \csc A=(65)/(16) \end{gathered}`

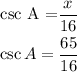
Therefore, the answer is

cscA = 65/16