Question

In one area, the lowest angle of elevation of the sun in winter is 21°. Find the distance x that a plant needing full sun can be placed from a fence that is 10.5 feet high. Round your answer to the tenthsplace when necessary.

Answer 1

The problem illustrated is a right-angled triangle.

Step 1: Label the sides of the triangle as shown:

Step 2: Using trigonometric ratios, find the required side

From trigonometric ratios, we have:

`\begin{gathered} sin\theta\text{ = }(opposite)/(hypothenuse) \\ cos\theta\text{ = }(adjacent)/(hypothenuse) \\ tan\theta\text{ = }(opposite)/(adjacent) \end{gathered}`

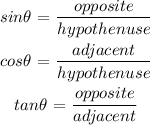
Using the tangent ratio, we can now find x:

`\begin{gathered} tan21\text{ = }(10.5)/(x) \\ x\text{ = }\frac{10.5}{tan\text{ 21}} \\ x\text{ = 27.35} \\ x\text{ }\approx\text{ 27.4} \end{gathered}`

Hence, the distance that a plant needs from the fence to get full sun is 27.4 feet