No 68
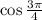
The angle 3pi/4 is in the 2nd quadrant, so
The value of cosine will be negative because in the 2nd quadrant only sine is positive
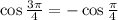
The value of cos pi/4 =
![\cos (\pi)/(4)=\frac{\sqrt[]{2}}{2}](https://img.qammunity.org/2023/formulas/mathematics/college/rtupeieh097yf914e8123teupbv5h6w89y.png)
So the answer is
![\cos (3\pi)/(4)=-\frac{\sqrt[]{2}}{2}](https://img.qammunity.org/2023/formulas/mathematics/college/dkkv3dgdqvsa7rs7dnwfj0t3n7xnzct5j3.png)
To solve this type of question, you should find the quadrant of the angle to know the sign of the function, then use the acute angle equivalent to this angle and find the value of the function and put the sign of the quadrant