Question

157) what is the largest number by which the expression n^3 - n is divisible for all possible integral values of n?

Answer 1

Q. 157:

We are given the following expression

`n^3-n`

Let us factor out the expression

`n^3-n=n(n^2-1)`

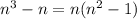
We can apply the difference of squares formula as shown below

`n(n^2-1^2)=n(n-1)(n+1)=(n-1)n(n+1)`

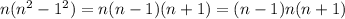
Notice that these are three consecutive integers (n-1), n, (n+1)

Since there are 2 consecutive integers, it must be divisible by 2.

Also, since there are 3 consecutive integers, it must be divisible by 3.

The LCM of 2, 3 is 6

Therefore, the largest number is 6 by which the given expression is divisible.