You have the following algebraic expression:
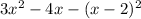
In order to simplify the previous expression you first expand the third term of the polynomial, that is, you expand the term (x-2)². In order to make the expansion, you use the following notable product:
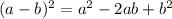
The, by taking into account the previous identity you obtain:
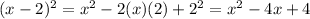
Next, you replace the last result into the given polynomial, as follow:
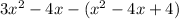
Eliminate parenthesis by using the rule for multiplication of signs:
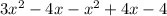
and finally, you simplify like terms:
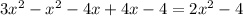
Hence, the simplified expression is 2x² - 4