Question

Find the equation of a line switch pass through the (12,6) and is parallel to the given line express your answer in slope intercept form simply your answer.

Answer 1

The equation of a line in the slope-intercept form is y = mx + b, where m is the slope and b is the y-intercept.

To solve this question, follow the steps below.

Step 01: Write the given equation in the slope-intercept form.

Given:

`4y-7=-2(4-2x)`

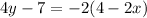
First, use the distributive property of multiplication:

`\begin{gathered} 4y-7=-2*4+(-2)*(-2x) \\ 4y-7=-8+4x \\ 4y-7=-8+4x \end{gathered}`

Add 7 to both sides.

`\begin{gathered} 4y-7+7=-8+4x+7 \\ 4y=-1+4x \end{gathered}`

Divide both sides by 4:

`\begin{gathered} (4y)/(4)=(4x-1)/(4) \\ y=x-(1)/(4) \end{gathered}`

Step 02: Find the slope of the second equation.

Given the lines are parallel, they have the same slope.

Thus, the slope is 1.

Then, the equation of the line is:

`\begin{gathered} y=1*x+b \\ y=x+b \end{gathered}`

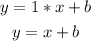
Step 03: Use the given point to find b.

Given the point (12, 6), substitute it in the equation to find b:

`6=12+b`

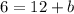
Subtracting 12 from both sides:

`\begin{gathered} 6-12=b+12-12 \\ -6=b \\ b=-6 \end{gathered}`

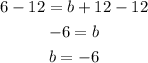
Thus, the equation of the line is:

`y=x-6`

Answer:

y = x - 6