Question

What is x the angle of depression in degrees round to hundredths

Answer 1

Let's begin by redrawing the diagram showing the angle of depression using the theory of corresponding angles:

Using trigonometric ratios, we have:

`\begin{gathered} \sin \text{ }\theta\text{ = }(opposite)/(hypothenuse) \\ \cos \text{ }\theta\text{ = }(adjacent)/(hypothenuse) \\ \tan \text{ }\theta\text{ = }(opposite)/(adjacent) \end{gathered}`

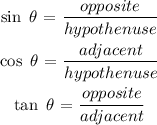
We have the sides:

opposite side = 27

adjacent side = 19

Since we have opposite and adjacent sides we would use the tangent ratio.

Substituting we have:

`\begin{gathered} \tan \text{ x = }(27)/(19) \\ x\text{ = }\tan ^(-1)((27)/(19)) \\ x\text{ = }54.8658 \\ \approx54.87^0\text{ (nearest hundredth)} \end{gathered}`

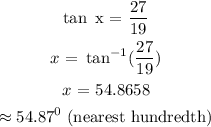
Answer: 54.87 degrees