First, we must take into account the definition of an odd function. A function f(x) is an odd function if it has the following property for all values of x:
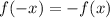
We can use this property to solve the exercise.
From the graph we read the following values for f:
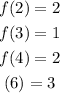
Using the data above and the property that defines odd functions we find:
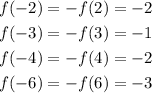
Answer
x f(x)
-2 -2
-3 -1
-4 -2
-6 -3