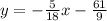Answer
Step-by-step explanation
The equation of the line can be given by the slope-intercept form:

where m is the slope and b is the y-intercept.
Additionally, parallel lines have the same slope, meaning that if the slope of the parallel line (to our line) is -5/18, then our slope is also -5/18, leaving us with the line:
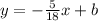
Next, we have to replace the values of the point (8, -9) given to:
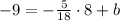
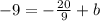
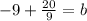
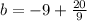
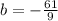
Finally, by rearranging the equation we get: