Question

For a lab for her Introductory Chemistry students, Dr. Fletcher needs 330 milliliters of 17%hydrochloric acid (HCI) solution. She currently has a 14% HCI solution and a 19% HCIsolution. How much of each solution should she mix together?

Answer 1

Let x be the volume of the 14% HCl solution and y the volume of the 19% HCl solution, in mililiters.

Since the total volume (in mililiters) of the mix should be 330, then:

`x+y=330`

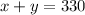
The total amount of HCl on the first mix is (14/100), on the second mix is (19/100)y and on the final mix, is (17/100)(330). Then:

`(14)/(100)x+(19)/(100)y=(17)/(100)\cdot330`

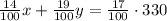
Isolate x from the first equation and substitute the resulting expression into the second one. Then, solve for y and go back to the first equation with the value of y to find the value of x:

`\begin{gathered} x+y=330 \\ \Rightarrow x=330-y \end{gathered}`
`\begin{gathered} (14)/(100)x+(19)/(100)y=(17)/(100)\cdot330 \\ \Rightarrow14x+19y=17\cdot330 \\ \Rightarrow14(330-y)+19y=17\cdot330 \\ \Rightarrow14\cdot330-14y+19y=17\cdot330 \\ \Rightarrow14\cdot330+5y=17\cdot330 \\ \Rightarrow5y=17\cdot330-14\cdot330 \\ \Rightarrow5y=(17-14)\cdot330 \\ \Rightarrow5y=3\cdot330 \\ \Rightarrow y=(3)/(5)\cdot330 \\ \Rightarrow y=198 \end{gathered}`
`\begin{gathered} x+y=330 \\ \Rightarrow x+198=330 \\ \Rightarrow x=330-198 \\ \Rightarrow x=132 \end{gathered}`

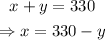
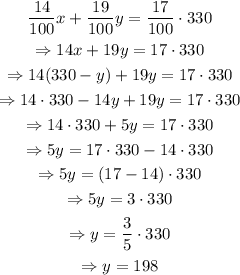
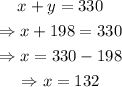
Therefore, 132 ml of 14% HCl solution and 198 ml of 19% HCl solution are needed to create 330 ml of 17% HCl solution.