Question

Use Cramer’s Rule to solve each system. 3. 3x-5y=4 6x+5y=23

Answer 1

Step-by-step explanation

We must solve the following system of equations using Cramer's Rule:

`\begin{gathered} 3x-5y=4 \\ 6x+5y=23 \end{gathered}`

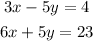
First we need to write it as a matrix equation of the form AX=B. The elements of A are the coefficients multiplying the variables in the equation, matrix X has the variables and B has the constants at the right of the equal signs:

`AX=\begin{bmatrix}{3} & {-5} \\ {6} & {5}\end{bmatrix}\begin{bmatrix}{x} \\ {y}\end{bmatrix}=\begin{bmatrix}{4} \\ {23}\end{bmatrix}=B`

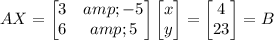
Cramer's rule requires the determinant of matrix A. Remember that for a 2x2 matrix the determinant is calculated as follows:

`det(\begin{bmatrix}{a} & {b} \\ {c} & {d}\end{bmatrix})=ad-bc`

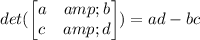
Then the determinant of A that we'll name D is:

`D=det(A)=3\cdot5-(-5)\cdot6=15+30=45`

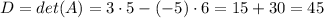
Now we have two construct two new matrices by replaceing each column of A with B. The first matrix that we'll name A' is given by taking the first column of A and replacing it with B. Then this matrix is:

`A^(\prime)=\begin{bmatrix}{4} & {-5} \\ {23} & {5}\end{bmatrix}`

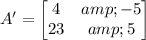
And its determinant D' is:

`D^(\prime)=det(A^(\prime))=4\cdot5-(-5)\cdot23=135`

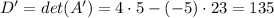
Since this matrix was built by replacing the first column which is the one associated with the variable x then the value of x is D'/D. Then we get:

`x=(D^(\prime))/(D)=(135)/(45)=3`

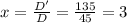
For y we are going to make a similar calculation but with the matrix A'' which is given by replacing the second column of A with matrix B:

`A^(\prime\prime)=\begin{bmatrix}{3} & 4{} \\ {6} & {23}\end{bmatrix}`

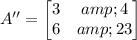
Its determinant D'' is:

`D^(\prime)^(\prime)=det(A^(\prime)^(\prime))=3\cdot23-4\cdot6=69-24=45`

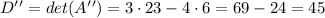
Then y is given by:

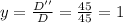
`y=(D^(\prime\prime))/(D)=(45)/(45)=1`Answer

Then the answers are x=3 and y=1.