Given data:
* The value of the potential energy given is,
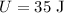
* The spring constant of the spring is,
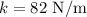
Solution:
The potential energy in terms of the compressed distance of the spring is,
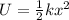
where x is the distance compressed,
Substituting the known values,
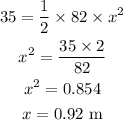
Thus, the spring is compressed to 0.92 m.