Question

6. A 3 kg object compresses a spring0.6m, giving it 8.1 J of energy.A. What kind of energy doos ithave?B. Calculate the spring constant for this spring.C. What kind of energy will the object have when thespring is released?

Answer 1

A.

Since the spring is compressed, it is storing potential elastic energy. This is a type of energy possessed by objects that are compressed and, when released, will create a force towards the equilibrium position.

B.

The spring constant can be calculated with the formula below:

`E_{\text{elastic}}=(kx^2)/(2)`

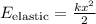
Where k is the spring constant and x is the deformation.

So, for E = 8.1 J and x = 0.6 m, we have:

`\begin{gathered} 8.1=(k\cdot0.6^2)/(2) \\ 16.2=k\cdot0.36 \\ k=(16.2)/(0.36) \\ k=45\text{ N/m} \end{gathered}`

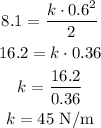
C.

When the spring is released, the potential elastic energy will be converted into kinetic energy to the object. This energy is related to movement: if the object has velocity, it has kinetic energy.