Solution
- The function given is:
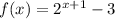
- The best way to understand the solution is to plot the function.
- The plot of the function is given below:
- From the above, we can already make the following deductions depicted below:
- Thus, we can answer the questions asked as follows:
Growth or Decay:
- This is clearly a GROWTH function as it increases from left to right.
- The reason for this increase is the term
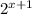
- 2 is the rate of change and since it is greater than 1, the function is increasing. If it were less than 1, it would be decay.
Domain:
- The domain is the set of all x-values for which the function is defined. The function has no breaks from left to right, thus, we can conclude that the domain is
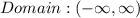
Range:
- The range is the set of all y-values for which the function is defined. The function has a minimum value of -3, which is also the Horizontal asymptote of the function. This is because,

Y-intercept:
- The y-intercept is simply where the graph crosses the y-axis. This also happens to be where x = 0 in the graph as well.
- From the figure above, we have that the y-intercept is (0, -1)
- But we can also get it from the equation by substituting the value of x = 0 into the function

Increasing Interval and Decreasing Interval:
- The interval for which the function is increasing is done by testing values of x and checking out the trend of the function. Usually, we test a negative value, x = 0, a positive value, then, negative and positive infinity.
- But since we have the graph plotted above, we can easily see that the graph is ALWAYS INCREASING over the interval
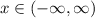
End behavior:
- The end behavior of the graph is simply the values of y as x tends to negative and positive infinity.
- Thus, we have:
