Question

Find the probability of selecting 3 cards from a standard deck withoutreplacing them and all 3 are hearts.A.11850B.14C.3132600D.164

Answer 1

In a deck, we have 52 cards and 13 heart cards. Let's calculate the probability of each event. The probability of getting a heart card with a full deck is just the amount of hearts divided by the total amount of cards.

`P_1=(13)/(52)`

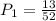
After drawing one heart card, now we have 51 cards in the deck and 12 of them are hearts(the 13 we started less the one we took). The probability for the second draw is:

`P_2=(12)/(51)`

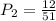
After the second draw, we have 50 cards and 11 hearts. By the same logic, the third probability is:

`P_3=(11)/(50)`

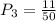
The probability that all those events happens simultaneously, is just their product.

`P_1* P_2* P_3=(13)/(52)*(12)/(51)*(11)/(50)=(1716)/(132600)`

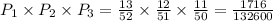
Simplifying this expression:

`(1716)/(132600)=(11)/(850)`

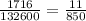
With this, we have our answer. The correct answer is the option A.