The volume of the box-shaped a cuboid is

l is the length
w is the width
h is the height
From the given figure
The volume of the box is 93 1/2 ft^3
V = 93 1/2
The width is 2 ft
w = 2
The height is 5 1/2 ft
h = 5 1/2
Substitute them in the rule above
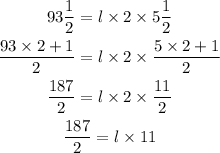
Multiply both sides by 2 to remove the denominator
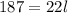
Divide both sides by 22 to find l
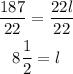
The length of the box is 8 1/2 ft
The answer is B