Question

A data set consisting of newborn baby weight is normally distributed with a mean of 8.5 pounds in standard deviation of 0.5 pounds

Answer 1

By the empirical rule, the 68% will lies between

`(\bar{x}-\sigma,\bar{x}+\sigma)`

Where

`\bar{x}=8.5\text{ and }\sigma=0.5`

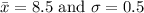
68% will lies between the interval

`\begin{gathered} (8.5-0.5,8.5+0.5) \\ (8.0,9.0) \end{gathered}`

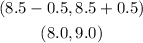
For the percentage that lies between 7.5 and 9.5 we will have

`\begin{gathered} 7.5=8.5-1=8.5-2(0.5)=\bar{x}-2\sigma \\ 9.5=8.5-1=8.5+2(0.5)=\bar{x}+2\sigma \end{gathered}`

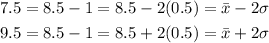
According to the empirical rule,

`\text{ 95\% of the data falls in the interval }(7.5,9.5)`

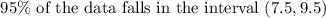
Therefore 95% will lies between 7.5 and 9.7 pounds

For the percentage that lies between 7 and 10 we will have

`\begin{gathered} 7=8.5-1.5=8.5-3(0.5)=\bar{x}-3\sigma \\ 10=8.5+1.5=8.5+3(0.5)=\bar{x}+3\sigma \end{gathered}`

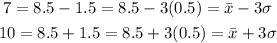
According to the empirical rule,

`\text{ 99.7\% of the data falls in the interval }(7,10)`

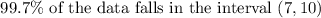
Therefore 99.7% lies between 7 and 10 pounds