Given data:
* The force acting on the particle is,
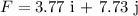
* The displacement of the particle along the x-axis is,
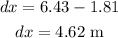
* The displacement of the particle along the y-axis is,
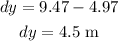
Solution:
The displacement vector of the particle is,
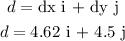
The work done on the particle in terms of the force and displacement vector is,
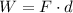
Substituting the known values,
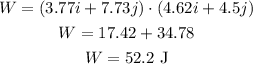
Thus, the work done by the force on the particle is 52.2 J.