Question

Not a timed or graded assignment. Please draw factor tree. As well as explanation/work for variables. Quick answer = amazing review :)

Answer 1

`30x^5\sqrt[]{-7x}`

Step-by-step explanation

We want to simplify the radical given by using a factor tree.

To do this, we have to draw the factor tree for the numeric term inside the radicand:

`63`

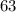
The factor tree is:

From the tree, we see that 63 can be rewritten as:

`\begin{gathered} 63=3\cdot3\cdot7 \\ 63=3^2\cdot7 \end{gathered}`

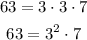
For the variable, we can simplify it as follows:

`\begin{gathered} x^(11)=x\cdot x\cdot x\cdot x\cdot x\cdot x\cdot x\cdot x\cdot x\cdot x\cdot x \\ \Rightarrow x^(11)=x^5\cdot x^5\cdot x \\ \Rightarrow x^(11)=(x^5)^2\cdot x \end{gathered}`

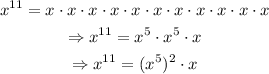
Hence, the simplified radical form of the given term is:

`\begin{gathered} 10\sqrt[]{-(3)^2\cdot7\cdot(x^5)^2\cdot x} \\ 10\cdot3\cdot x^5\cdot\sqrt[]{-7\cdot x} \\ \Rightarrow30x^5\sqrt[]{-7x} \end{gathered}`

That is the answer.