Answer:
y=-3x+5
Explanation:
Given a line L such that:
• L has y-intercept (0,5); and
,
• L is perpendicular to the line with equation y=(1/3)x+1.
We want to find the equation of the line in the slope-intercept form.
The slope-intercept form of the equation of a straight line is given as:

Comparing the given line with the form above:
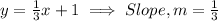
Next, we find the slope of the perpendicular line L.
• Two lines are perpendicular if the product of their slopes is -1.
Let the slope of L = m1.
Since L and y=(1/3)x+1 are perpendicular, therefore:
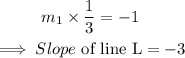
The y-intercept of L is at (0,5), therefore:
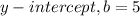
Substitute the slope, m=-3, and y-intercept, b=5 into the slope-intercept form.
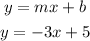
The equation of line L is:
