Given :
Circle with center : (3, -5)
radius : 7
The equation of a circle with center (a,b) and radius r is given as :

The equation of the circle with center (3, -5) and radius 7 is :
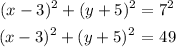
The points that lie on the circle can be found by substituting the points into the equation
for (-2, -3)
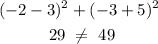
for (3, -5)
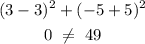
for (3,2)
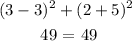
For (10, -5)
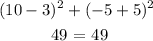
for (10, 2)
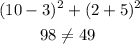
Hence, the points that lie on a circle are : (3,2) and (10, -5)