Answer:
y=ax-(3a+5).
Step-by-step explanation:
Given the line:
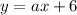
Comparing with the slope-intercept form: y=mx+b
• The slope of the line, m = a.
Two lines are parallel if they have the same slope.
Thus, we find the equation of a line with:
• Slope, m=a
,
• Point, (x1,y1)=(3,-5)
Using the point-slope form:
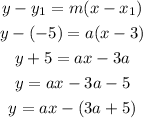
The equation of the line is y=ax-(3a+5).