Question

A depositor opens a new savings account with $4000 at 8% compounded semiannually. At the beginning of your 4, an additional 55000 is deposited. At the end of fiveyears, what is the balance in the account?

Answer 1

For the first 3 years, the principal or amount deposited was $4000

It was compunded semiannually for the first 3 years

We would apply the formula for determining compound interest which is expressed as

`A\text{ = P(1 + }(r)/(n))^(nt)`

A = amount after t years

P = principal

t = number of years

r = interest rate

n = periodic interval at which the principal was compounded

Therefore, for the first 3 years,

t = 3 years

P = $4000

r = 8% = 8/100 = 0.08

n = 2(two times in a year)

Therefore,

`\begin{gathered} A\text{ = 4000(1 + }(0.08)/(2))^(2*3) \\ A=4000(1.04)^6 \\ A\text{ = }5061.27 \end{gathered}`

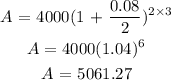
At the begining of the 4th year, $55000 was deposited. The new principal would be

55000 + 5061.27 = $60061.27

The number of years between the 4th and the 5th year is one. Thus, t = 1 year

Therefore

`\begin{gathered} A=60061.27(1.04)^(2*1) \\ A\text{ = }60061.27(1.04)^2 \\ A\text{ = 64962.27} \end{gathered}`

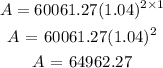
The balance in the account after 5 years is $64962.27