We will do first the diagram
total fence used 840 ft
The total fence in terms of the variables
3y+2x=840
then we isolate the y
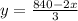
then we calculate the area
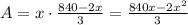
then we have a quadratic equation, which means that the max will be the vertex
the
x coordinate of the vertex can be calculated
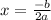
where
a=-2
b=840
we substitute the values
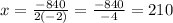
then we susbtitute in the function of the area
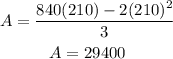
then we find y
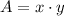
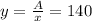
The dimensions that maximize the enclosed area
x=210 ft
y=140ft
The maximum area is 29400 ft^2