Question

Thirty students in the fifth grade class listed their hair and eye colors in the table below:Are the events "brown hair" and "brown eyes" independent? A.) Yes, P(brown hair) ⋅ P(brown eyes) = P(brown hair ∩ brown eyes)B.) Yes, P(brown hair) ⋅ P(brown eyes) ≠ P(brown hair ∩ brown eyes)C.) No, P(brown hair) ⋅ P(brown eyes) = P(brown hair ∩ brown eyes)D.) No, P(brown hair) ⋅ P(brown eyes) ≠ P(brown hair ∩ brown eyes)

Answer 1

Let us begin by defining an independent event

Two events A and B are said to be independent if the fact that one event has occurred does not affect the probability that the other event will occur.

For independent events A and B:

`P(A\text{ and B\rparen = P\lparen A\rparen }*\text{ P\lparen B\rparen}`

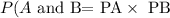
The two events under study are

- Brown hair

- Brown eyes

The probability of a brown hair:

`P(brown\text{ hair\rparen = }(19)/(30)`

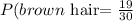
The probability of brown eyes:

`P(brown\text{ eyes\rparen = }(15)/(30)`

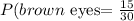
The probability of brown hair and brown eyes:

`P(brown\text{ hair and brown eyes\rparen = }(10)/(30)`

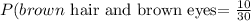
Check:

The events would be independent if:

`P(brown\text{ hair and brown eyes\rparen = P\lparen brown hair\rparen }*\text{ P\lparen brown eyes\rparen}`
`\frac{10}{30\text{ }}\text{ }\\e(19)/(30)\text{ }*(15)/(30)`

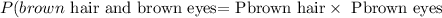
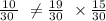
Hence, the correct option is No, P(brown hair) . P(brown eyes) ≠ P(brown hair ∩ brown eyes)

Answer: Option D