Question

Complete the square to make a perfect trinomial. Write the result as a binomial squared

Answer 1

We have the expression:

`a^2-(a)/(2)+C^2`

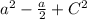
We have to find the third term C², the independent term, in order for this expression to be a perfect trinomial.

We can express the square of a binomial as:

`(x+y)^2=x^2+2xy+y^2`

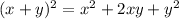
So in this case, one term of the binomial will be "a".

Then, if we compare it to our expression, the term in the middle (2xy) would be twice the product of a and C.

If we write the equation we obtain:

`-(a)/(2)=2aC`

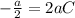
We can use it to find the value of C as:

`\begin{gathered} -(a)/(2)=2aC \\ -(1)/(2)=2C \\ C=-(1)/(4) \\ \Rightarrow C^2=(-(1)/(4))^2=(1)/(16) \end{gathered}`

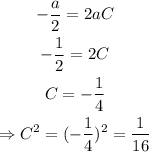
Then, we can write the binomial as:

`a^2-(a)/(2)+(1)/(16)=(a-(1)/(4))^2`

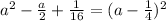
Answer:

a² - a/2 + 1/16 = (a - 1/4)²