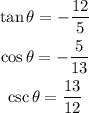It is given that the terminal side of angle θ passes through the point (-5/13, 12/13) in quadrant II on a unit circle.
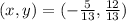
Let us find the given trigonometric ratios in the simplest rational form.
First, we need to find the hypotenuse side using the Pythagorean theorem.
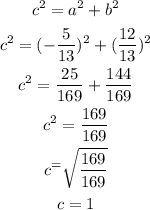
So, the hypotenuse side is 1.
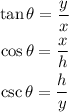
Where
x = -5/13
y = 12/13
h = 1
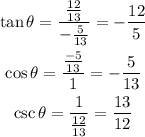
Therefore, the trigonometric ratios in the simplest rational form are