Question

Let A ( ) f (t )dt where f is the function given by the graph below

Answer 1

To solve the problem, we need to understand the integral as the sum of areas under/over the graph of the function.

If the area is above the x-axis, the area is considered positive, otherwise, it's negative.

The function A(x) is defined as:

`A(x)=\int_1^xf(t)dt`

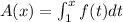
Find A(2):

`A(2)=\int_1^2f(t)dt`

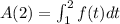
The integral from t = 1 to t = 2 is the area of the triangle of base b = 1 unit and height h = 1 unit. Thus the area is:

`A=(bh)/(2)=(1\cdot1)/(2)=(1)/(2)`

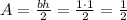
Thus:

A(2) = 1/2

Find A(8):

`A(8)=\int_1^8f(t)dt`

We have to find the area of the graph from t = 1 to t = 8. Note that the triangle from t =1 to t = 2 has the same dimensions as the triangle from t =2 to t = 3, but the first one is above the x-axis and the second is below, so they cancel out.

We only need to calculate the area from t = 3 to t = 8.

There we have a rectangle of length 8 - 3 = 5 units and a width of -1 unit.

The area of the rectangle is:

A = 5 x (-1) = -5, thus:

A(8) = -5