In order to prove this is a right triangle, we can find the length of each side and then verify if they suit the Pythagorean Theorem.
First, to find those lengths, we will use the formula:
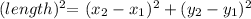
Since this triangle is formed by the points A(3, 4), B(1, 1), and C(-2, 3), we have:
a² = (BC)² = (-2 - 1)² + (3 - 1)² = (-3)² + 2² = 9 + 4 = 13
b² = (CA)² = (3 - (-2) )² + (4 - 3)² = 5² + 1² = 25 + 1 = 26
c² = (AB)² = (1 - 3)² + (1 - 4)² = (-2)² + (-3)² = 4 + 9 = 13
Now, the Pythagorean Theorem says:
H² = (leg1)² + (leg2)²
where H, the hypotenuse, is the larger side of the triangle. Then we have to verify if
b² = a² + b²
26 = 13 + 13
Since the above expression is indeed equality, this triangle satisfies the Pythagorean Theorem. Therefore, ABC is a right triangle.