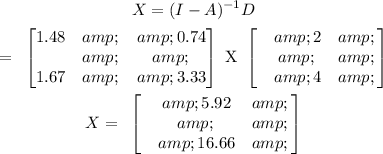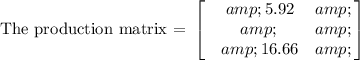Let the production matrix = X
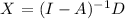
Next
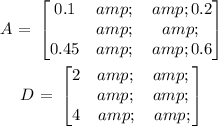
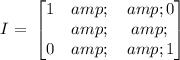
Next, evaluate X
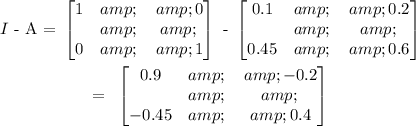
Next, you find the inverse of I - A which is adjount of I - A divided by it determinant.
Determinant of (I - A) = 0.9 x 0.4 - (-0.45 x -0.2) = 0.36 - 0.09 = 0.27
Adjount of (I - A) is the transpose of it co-factor
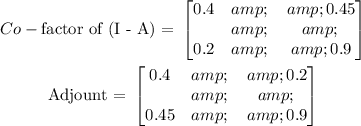
Therefore
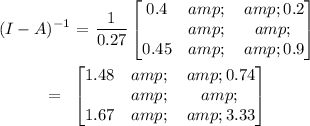
Now, we find x