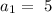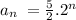Question: Use the geometric sequence to help write a recursive rule and an explicit rule for any geometric sequence:
Solution:
A geometric sequence is a sequence of numbers in which the ratio between consecutive terms is constant. Remember that the constant factor (ratio) between consecutive terms of a geometric sequence is called the common ratio. Now, given a geometric sequence with the first term a1 and the common ratio r, the nth (or general) term is given by:
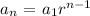
Thus, in this case, the common ratio r is:

On the other hand, the first term of the sequence is a1 = 5. Then, we can conclude that the explicit rule for the given sequence is:
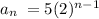
this is equivalent to:

this is equivalent to:
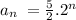
Then, the correct answer is:
The general rule:
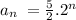
the recursive rule: