a) 2
b) 10
Step-by-step explanation:
The values of x and y given:
X has 0, 2, 4, 6, 8, 10
Y has 0, -4, 0, 12, 32, and 60
We are to find the average rate of change using the formula:
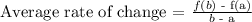
a) from x = 0 to x = 6
let b = 6, a = 0
We need to check the corresponding y values for x = 0 and x = 6
when x = 0, y = 0; f(a) = 0
when x = 6, y = 12; f(b) = 12
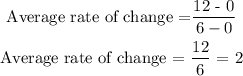
b) 4 less than or equal to X less than or equal to 10
This is written as:
4 ≤ x ≤10
a = 4, b = 10
We need to check the corresponding y values for x = 4, and x = 10
when x = 4, y = 0; f(a) = 0
when x = 10, y = 60; f(b) = 60
