1 Answer

Merrill Cook · Answer 1 · 2023-11-18T00:17:16+0000

We have that the quadratic expression is given by:

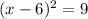
If we apply the square root to both sides of the equation, we have:

$\sqrt[]{(x-6)^2}=\pm\sqrt[]{9}$

As we can see, we will have two solutions. Then, we have:

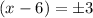
$(x-6)=\pm3_{}$

Then, we have the two possible solutions as follows:

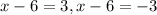
And we need to solve for both of them as follows:

First case

1. We need to add 6 to both sides of the equation:

$x-6=3\Rightarrow x-6+6=3+6\Rightarrow x=9$

2. We need to add 6 to both sides of the equation:

$x-6=-3\Rightarrow x-6+6=-3+6\Rightarrow x=3_{}$

Therefore, in summary, the exact answers are x = 9, and x = 3.