Question

Write an Equation for the line in point-slope form. Then rewrite the equation in slope-intercept form.(3,-8),(-2,5)

Answer 1

Let's recall the general formof the equation of a line in point-slope form:

`y-y_1=m(x-x_1)`

where x1 and y1 are the coordinates of the point (x1, y1) the line foes through, and m is the slope.

So,we need to start by finding the slope os a segment that joins the points they gave us: (3 , -8) and (-2, 5)

So we use the formula for slope:

`\text{slope}=(y_2-y_1)/(x_2-x_1)`

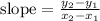
which in our case becomes:

slope = (5 -(-8)) / (-2-3) = 13/(-5) = - 13/5

Now we have the equation of the line in point-slope form by using for example point (-2, 5) as our selected point:

`y-5=-(13)/(5)(x+2)`

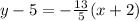
Therefore the equation in point-slope form is:

y - 5 = - (13/5) ( x + 2 )

And now, we can write this equation in slope-intercept form by simple solving for y and performing all implicit operations on the right:

`\begin{gathered} y-5=-(13)/(5)(x+2) \\ y-5=-(13)/(5)x-(26)/(5) \\ y=-(13)/(5)x-(26)/(5)+5 \\ y=-(13)/(5)x-(1)/(5) \\ \end{gathered}`

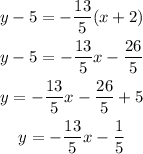
Therefore, the equation in slope-intercept becomes:

y = - (13/5) x - (1/5)