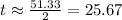Answer: 25.7 seconds
Step-by-step explanation
Equation
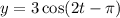
where y is the displacement in feet and t is time in seconds.
We are asked to find t when y = 2ft, meaning that we have to solve the equation for t:
0. Replacing the information given by setting the equation to 2:
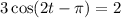
2. Dividing both sides of the equation against 3 and simplifying:
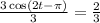
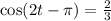
2. Applying secant (cos⁻¹) to both sides:
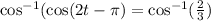
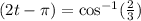
3. Adding π to both sides of the equation:
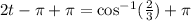
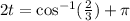
4. Dividing both sides of the equation against two:
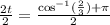
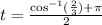
5. Simplifying we get: