Answer:
D) 82.57
Explanation:
Area of the semicircle:
The area of a semicircle is given by:
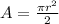
In which r is the radius.
In the semicircle in this question, the diameter is 10. The radius is half the diameter, so r = 10/2 = 5.
Then
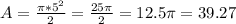
Area of the equilateral triangle:
The area of an equilateral triangle with side s is given by:
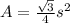
In this question, s = 10. So
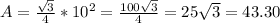
Total area:
Sum of the semicircle with the equilateral triangle.
A = 39.27 + 43.30 = 82.57
The correct answer is:
D) 82.57