Question

The figure in the diagram is composed of a semi-circle and an equilateral triangle. Find the total area of the figure.

Answer 1

D) 82.57

Explanation:

Area of the semicircle:

The area of a semicircle is given by:

`A=(\pi r^2)/(2)`

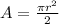
In which r is the radius.

In the semicircle in this question, the diameter is 10. The radius is half the diameter, so r = 10/2 = 5.

Then

`A=(\pi\ast5^2)/(2)=(25\pi)/(2)=12.5\pi=39.27`

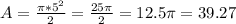
Area of the equilateral triangle:

The area of an equilateral triangle with side s is given by:

`A=(√(3))/(4)s^2`

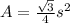
In this question, s = 10. So

`A=(√(3))/(4)\ast10^2=(100√(3))/(4)=25√(3)=43.30`

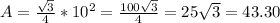
Total area:

Sum of the semicircle with the equilateral triangle.

A = 39.27 + 43.30 = 82.57

The correct answer is:

D) 82.57