From the given information, we know that
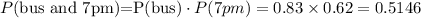
because they are independent events. Similarly, we have
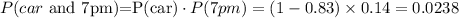
Now, we need the conditional probability P(bus | 7pm), which can be given as
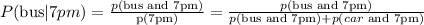
By substituting our result into this last expression, we get
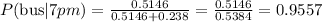
By rounding up our result, the answer is 0.96, which corresponds to 96 %