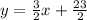Question

Find the equation of the line that passes through the point (-3,7) and is perpendicular to y= -2/3x-6Give your answer in slope-intercept form.

Answer 1

To determine the equation of a line we need to know at least two points the said line passes through or one point and its slope.

We know one point and the equation of a line perpendicular to the one we are looking for.

If two lines are perpendicular, then their slopes are negative reciprocals of each other. This means that the slope of the line we have to establish is the negative inverse of the slope of the line we know.

The given line is:

`y=-(2)/(3)x-6`

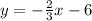
Its slope is the coefficient that multiplies the x-value, so m=-2/3

To determine the slope of the perpendicular line you have to invert the fraction and multiply it by -1

`m_2=-(1)/(m_1)=-(-(3)/(2))=(3)/(2)`

m₁ is the slope of the known line

m₂ is the slope of the perpendicular line

Now that we have determined the slope of the perpendicular line, we can use the point-slope form to calculate its equation

`y-y_1=m(x-x_1)`

Where

m is the slope of the line

(x₁,y₁) are the coordinates of one point on the line

Using m=3/2 and the point (-3,7) the equation in point-slope form is

`\begin{gathered} y-7=(3)/(2)(x-(-3)) \\ y-7=(3)/(2)(x+3) \end{gathered}`

To express the equation in the slope-intercept form you have to leave y on the right side of the equation and all other terms on the right side.

-First, distribute the multiplication on the parentheses term:

`\begin{gathered} y-7=(3)/(2)\cdot x+(3)/(2)\cdot3) \\ y-7=(3)/(2)x+(9)/(2) \end{gathered}`

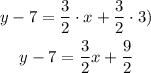
-Second, pass "-7" to the other side of the equation by applying the opposite operation to both sides of it and simplify the like terms:

`\begin{gathered} y-7+7=(3)/(2)x+(9)/(2)+7 \\ y=(3)/(2)x+(23)/(2) \end{gathered}`

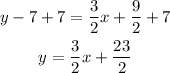
The equation of the line that passes through (-3,7) and is perpendicular to y=-2/3x-6 is

`y=(3)/(2)x+(23)/(2)`