Solution:
Let V represent the rate of the airplane, let W represent the rate of the wind.
But

Thus, against the direction of wind, we have

When the airplane is in the direction of wind, we have

From equation 1, make V the subject of the formula or equation.
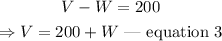
Substitute equation 3 into equation 2.
Thus, we have

Substitute the value of 60 for W into equation 3.
Recall that
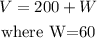
Thus,
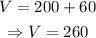
Hence, the airplane flies at 260 mi/h with no wind. The rate of wind is 60 mi/h.
The first option is the correct answer.