Given data:
The height of the building is h=12 m.
The pressure on the ground is
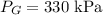
The water pressure at the ground level can be given as,
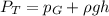
Here,
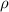
is the density of water whose value is
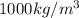
and g is the gravity whose value is
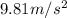
Substituting the values in the above equation, we get:
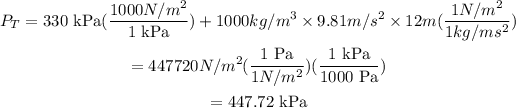
Thus, the water pressure at the ground level is 447.72 kPa.