Step 1
Using the given translations, find the equation for circle O'

That is the equation of circle O' becomes

From the image the green circle is that of circle O and the blue circle is that of circle O'
Equation of the new circle is
(x + 2)² + (y - 1)² = 16
Step 1: Dilate the circle O' by a scale factor of 3 to get a new circle O"
To dilate the circle O', we multiply the right side of the equation of circle O' by 3² to get:
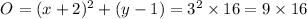
Equation of the new circle after dilation becomes
O": (x + 2)² + (y - 1)² = 144