The given equation:
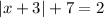
can be simplified as follow
Step 1: collect like terms
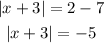
Step 2: Sice the equation involves absolute values,
assume two cases
case 1: take the result of the left-hand side to be positive so that
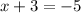
Then
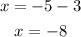
Case 2: take the result of the left-hand side to be negative so that

then
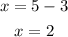
Step 3: Check if the values of x obtained in step 2 satisfy the original equation
when x=-8

Then x=-8 is not a solution
Similarly
when x=2

Also, x=2 is not a solution,
therefore
The equation has no solution