Question

21State if the pair of triangles aresimilar, if so, state the similaritycriteria (SSS, SAS, or AA)17A31RB 40S>64

Answer 1

Since the ratio of the sides are not equal then the triangles are not similar

`(AS)/(BS)\\e(QS)/(RS)`

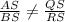
Step-by-step explanation:

Given the figure in the attached image.

We want to confirm if the triangles are similar.

The only common angle to the two triangles is angle S.

And there is no information on the similarities of other angles.

If the two triangles are similar the ratio of their sides will be equal;

`(AS)/(BS)=(QS)/(RS)`

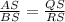
Given;

`\begin{gathered} AS=31 \\ BS=40 \\ QS=31+17=48 \\ RS=64 \end{gathered}`

substituting the values;

`\begin{gathered} (AS)/(BS)=(31)/(40)=0.775 \\ (QS)/(RS)=(48)/(64)=0.75 \\ \therefore \\ (AS)/(BS)\\e(QS)/(RS) \end{gathered}`

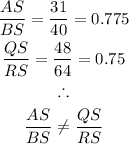
Therefore, since the ratio of the sides are not equal then the triangles are not similar