Question

In A ABC, mZA = 3x + 1; mZB = 4x - 17, andmZC = 5x – 20. Which type of triangle is AABC?1) right2) scalene3) isosceles4) equilateral

Answer 1

We can calculate the values of the angles given that the sum of the interior angles is equal to 180 degrees:

`\begin{gathered} mA+mB+mC=180 \\ (3x+1)+(4x-17)+(5x-20)=180 \\ 12x-36=180 \\ 12(x-3)=180 \\ x-3=(180)/(12) \\ x-3=15 \\ x=15+3 \\ x=18 \end{gathered}`

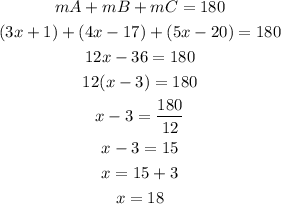
With the value of x, we can calculate the value of each of the angles:

`\begin{gathered} mA=3\cdot18+1=54+1=55 \\ mB=4\cdot18-17=72-17=55 \\ mC=5\cdot18-20=90-20=70 \end{gathered}`

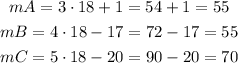
As we have 2 equal angles, we can think of the triangle as having a axis of symmetry, bisecting the angle that has a unique value (mC=70 deg).

Then, as we have an axis of symmetry, two of the sides of the triangle are equal.

Then, the triangle is isosceles (Option 3).