Question

A man flies a small airplane from Fargo to Bismarck, North Dakota a distance of 180 miles. Because he is flying into a head wind, the trio takes him 2 hours. On the way back, the wind is still blowing at the same speed so the return trip takes only 1 hour and 30 minutes. what is the plane's speed in still air, and how fast is the wind blowing his plane speed equals _____ mph the wind speed equals ______ mph

Answer 1

Let the planes speed = x

And the wind speed = y

The distance = 180 miles

Speed = distance over the time

On the go :

Time = 2 hours

so,

`\begin{gathered} x-y=(180)/(2) \\ x-y=90 \end{gathered}`

On the way back, the wind is still blowing at the same speed so the return trip takes only 1 hour and 30 minutes.

Time = 1.5 hours

`x+y=(180)/(1.5)=120`

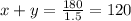
so, we have the following system of equations:

`\begin{gathered} x-y=90\rightarrow(1) \\ x+y=120\rightarrow(2) \\ ----------- \\ 2x+(y-y)=90+120 \\ 2x=210 \\ x=(210)/(2)=105 \\ y=105-90=15 \end{gathered}`

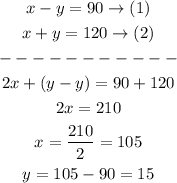
So, the answer is:

his plane speed equals 105 mph

the wind speed equals 15 mph​