Question

What is the equation of the circle whose diameter has endpoints (9,1) and (9,15)

Answer 1

`\text{The equation }of\text{ circle: }(x-9)^2+(y-8)^2=49`

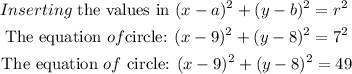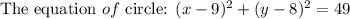
Step-by-step explanation:

Given endpoints (9,1) and (9,15)

The equation of circle:

`(x-a)^2+(y-b)^2=r^2`

To find (a, b) which is the center of the circle, we will apply the midpoint formula:

`\text{Midpoint = }(1)/(2)(x_1+x_2),\text{ }(1)/(2)(y_1+y_2)`

`\begin{gathered} \text{Midpoint =1/2}(9+9),\text{ 1/2(1+15) } \\ Midpoint=\text{ 9, 8} \\ \text{Center = }(a,\text{ b) = 9, 8} \end{gathered}`

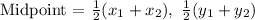
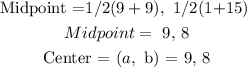
To find the radius (r), we need to find the distance between the center an any of the two points.

Using (9, 8) and (9, 1)

`dis\tan ce\text{ formula= }\sqrt[]{(y_2-y_1)^2+(x_2-x_1)^2}`
`\begin{gathered} \text{distance = }\sqrt[]{(1-8)^2+(9-9)^2} \\ =\text{ }\sqrt[]{(-7)^2+(0)^2}\text{ = }\sqrt[]{49+0} \\ \text{Distance = }\sqrt[]{49\text{ }}=\text{ 7} \\ \text{radius = 7} \end{gathered}`
`\begin{gathered} Inserting\text{ the values in }(x-a)^2+(y-b)^2=r^2\text{ } \\ \text{The equation }of\text{circle: }(x-9)^2+(y-8)^2=7^2 \\ \text{The equation }of\text{ circle: }(x-9)^2+(y-8)^2=49 \end{gathered}`