Question

Jade is going shopping. She wants to buy a jacket for $25 and a few shirts that cost $11 each. She wants to spend less than $80.

Answer 1

Let J be the jacket and S the shirts. Jade wants to know how many shirts she can buy.

Then, we can write the following relationship:

`25\cdot J+11\cdot S=80`

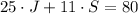
since Jade only wants one jacket, this means that J=1. Then, by substituting these value into our formula, we have

`25\cdot1+11\cdot S=80`

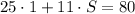
which gives

`25+11S=80`

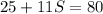
Now, if we move 25 to the right hand side as -25, we obtain

`\begin{gathered} 11S=80-25 \\ 11S=55 \end{gathered}`

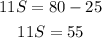
and finally, we have

`\begin{gathered} S=(55)/(11) \\ S=5 \end{gathered}`

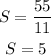
that is, Jade can buy 5 shirts and 1 jacket with $80.