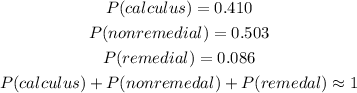Question

Many colleges require students to take a placement exam to determine which math courses they are eligible to take during the first semester of their freshman year. Of the 2938 freshmen at a local state college, 254 were required to take a remedial math course, 1478 could take a nonremedial, non-calculus-based math course, and 1206 could take a calculus-based math course.a. If one of the freshmen is selected at random, find the probability that this student could take a calculus-based math course.Round your answer to three decimal places.P(the student taking a calculus-based math course)= Enter you answer; P(the student taking a calculus-based math course) b. If one of the freshmen is selected at random, find the probability that this student could take a nonremedial, non-calculus-based math course.Round your answer to three decimal places.P(the student taking a nonremedial, non-calculus-based math course)= Enter you answer; P(the student taking a nonremedial, non-calculus-based math course) c. If one of the freshmen is selected at random, find the probability that this student could take a remedial math course.Round your answer to three decimal places.P(the student taking a remedial math course)= Enter you answer; P(the student taking a remedial math course) Should these probabilities add up to 1.0?Choose your answer; Should these probabilities add up to 1.0?eTextbook and MediaAttempts: 0 of 5 used

Answer 1

Given:

Total number of students = 2938

Number of remedial math course students = 254

Number of nonremedial math course students = 1478

Number of calculus-based math = 1206

Required:

(1) Find the probability that this student could take a calculus-based math course.

(2) Find the probability that this student could take a nonremedial, non-calculus-based math course.

(3) find the probability that this student could take a remedial math course.

Step-by-step explanation:

The probability formula for an event is given as:

`P=\frac{Number\text{ of possible outcomes}}{Total\text{ number of outcomes}}`

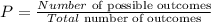
(1) The probability that this student could take a calculus-based math course.

`\begin{gathered} P(calculus)=(1206)/(2938) \\ P(calculus)=0.410 \end{gathered}`

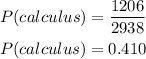
(2) The probability that this student could take a nonremedial, non-calculus-based math course.

`\begin{gathered} P(nonremedial)=(1478)/(2938) \\ P(nonremedial)=0.503 \end{gathered}`

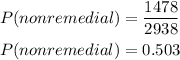
(3) the probability that this student could take a remedial math course.

`\begin{gathered} P(remedial)=(254)/(2938) \\ P(remedial)=0.086 \end{gathered}`
`\begin{gathered} P(remedial)=(254)/(2938) \\ P(remedial)=0.086 \end{gathered}`
`\begin{gathered} P(calculus)+P(nonremedial)+P(remedial)=0.410+0.503+0.086 \\ P(calculus)+P(nonremedial)+P(remedial)=0.999 \\ P(calculus)+P(nonremedial)+P(remedial)\approx1 \end{gathered}`

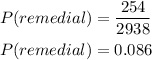
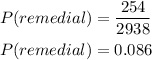
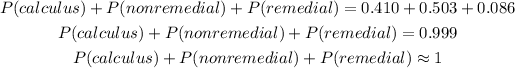
Final answer:

`\begin{gathered} P(calculus)=0.410 \\ P(nonremedial)=0.503 \\ P(remedial)=0.086 \\ P(calculus)+P(nonremed\imaginaryI al)+P(remed\imaginaryI al)\approx1 \end{gathered}`